
图源:Pixabay
撰文 | 丁玖
在《知识分子》刊载的《数学战争警示录:我们需要什么样的数学教育?》一文中,'数学战争'这个比喻引发了广泛讨论。这场持续数十年的教育理念之争,不仅塑造了北美数学教育的特殊面貌,更直接影响着一代代美国学生的数学素养。当全球教育者都在思考'如何培养适应未来的数学人才'时,美国教育体系的经验教训显得尤为珍贵。
2025年,当我结束在美国公立大学35年的教学生涯时,这个国家从小学到大学的数学教育图景已清晰呈现。1986年元旦,我作为密歇根州立大学数学系博士生首次站上美国讲台,这种跨文化的教学体验很快颠覆了我对发达国家教育的想象。
在为物理系新生讲授初等微积分时,我遭遇了令人震惊的教学困境:学生反复询问多项式导数运算这类基础问题,一元二次方程求根公式竟成为多数人的知识盲区。更令人匪夷所思的是1986年10月9日的监考经历——当看到学生将'14-5'计算为11并坚持己见时,作为教育者的挫败感达到顶点。这种在小学阶段就该掌握的算术能力缺失,折射出美国基础数学教育的系统性危机。
这种认知差异并非个案。十年后,我在某著名私立文理学院的朋友透露,即便这所培养过宋美龄、希拉里等杰出人才的学府,其毕业生也普遍存在代数基础薄弱的问题。这种看似矛盾的现象,实则暴露了美国精英教育与大众教育之间的深刻断裂。

图源:Pixabay
美国数学教育的困境,本质上是两种教育哲学的激烈碰撞。以杜威实用主义为源头的进步主义教育派,与坚持学科本质的传统数学教育派,自二十世纪初就开始了持续百年的理念交锋。这种争论在1980年国家数学教师委员会《行动的规则》报告中达到高潮——该报告主张'问题解决优先于技能掌握',甚至建议小学生使用计算器替代手工计算。
1989年的《学校数学课程和测试标准》将这种理念推向极端。在24名制定者中仅2名中小学教师且无数学家参与的情况下,这份'去技能化'的标准却在全国推广。其核心主张包括:弱化代数几何的分类教学,采用'综合数学'模式;降低高中代数要求;用'探索式发现'取代系统知识传授。这种教育实验的直接后果,是造就了'不会解方程的工程师'和'不懂几何证明的数学家'。
数学家群体的反抗在二十世纪末达到高潮。华裔几何学家伍鸿熙教授在加州教育会议上,当面批评教育学家编写的教材'违背数学逻辑',成为这场战争的标志性事件。但四十年来,尽管里根政府《危险中的国家》报告早已警示'教育平庸化威胁国家未来',美国基础教育仍未能走出困境。
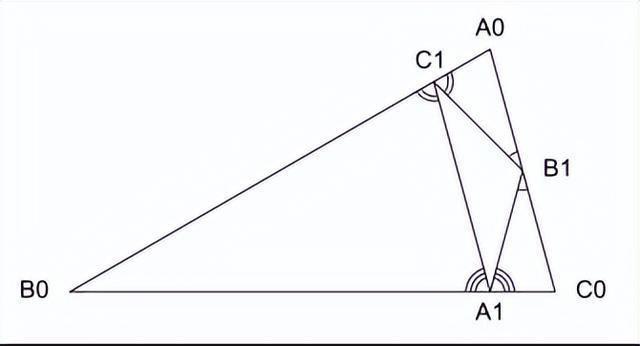
美国数学教育的深层危机,在师资培养环节暴露无遗。在教授研究生课程时,我多次遇到在职高中数学教师参与培训。当讲解'垂足三角形'分形构造时,这些攻读数学教育硕士的教师竟无人能证明基础几何命题——这在中国中学课堂属于必须掌握的核心技能。
这种师资缺陷源于系统性的培养缺失:美国小学教师普遍不要求背诵乘法口诀表,中学教师解方程需分五步演示,高中几何教材删减推理证明内容。当'探索式学习'取代'逻辑训练',学生失去的不仅是计算能力,更是数学思维的核心——逻辑推理能力。这解释了为何我的高等微积分课程中,70%学生无法解决关于数集上确界的基本问题。
尽管大众教育存在严重缺陷,美国对资优教育的投入却堪称极致。每所普通高中都为顶尖学生开设AP微积分等大学先修课程,斯坦福等精英大学的数学尖子表现常优于中国名校学生。这种'自由放任与重点培养并存'的模式,既造就了科技创新的领军人物,也放任了大多数学生的数学能力滑坡。
美国四十年的教育实验提供了宝贵教训:有效的数学教育必须遵循'基础扎实→技能熟练→创新应用'的逻辑链条。基础知识是创新基石,基本技能是应用关键,二者缺一不可。那种试图通过'探索式学习'跳过系统训练的做法,只会培养出'好高骛远却基础薄弱'的学习者。
对中国教育者而言,美国经验启示我们:既要警惕'去技能化'的诱惑,坚持数学思维的逻辑训练;也要借鉴其资优教育经验,为顶尖人才提供发展空间。在人工智能时代,数学教育更需要平衡'基础巩固'与'创新培养',这才是通向教育强国的正确道路。
